Primitive Root

Primitive Root of a Prime number
The primitive root 'g' of a prime number is such that 'p' and 'g' are COPRIME i.e. GCD(p,g)=1.
and  is congruent to a power of g modulo n. 


Ex.
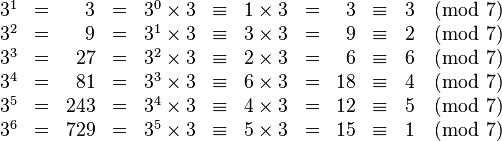
\begin{array}{rcrcrcrcrcr} 3^1 &=& 3 &=& 3^0 \times 3 &\equiv& 1 \times 3 &=& 3 &\equiv& 3 \pmod 7 \\ 3^2 &=& 9 &=& 3^1 \times 3 &\equiv& 3 \times 3 &=& 9 &\equiv& 2 \pmod 7 \\ 3^3 &=& 27 &=& 3^2 \times 3 &\equiv& 2 \times 3 &=& 6 &\equiv& 6 \pmod 7 \\ 3^4 &=& 81 &=& 3^3 \times 3 &\equiv& 6 \times 3 &=& 18 &\equiv& 4 \pmod 7 \\ 3^5 &=& 243 &=& 3^4 \times 3 &\equiv& 4 \times 3 &=& 12 &\equiv& 5 \pmod 7 \\ 3^6 &=& 729 &=& 3^5 \times 3 &\equiv& 5 \times 3 &=& 15 &\equiv& 1 \pmod 7 \\ \end{array}


Here we see that the period of 3k modulo 7 is 6. The remainders in the period, which are 3, 2, 6, 4, 5, 1, form a rearrangement of all nonzero remainders modulo 7, implying that 3 is indeed a primitive root modulo 7.


Ex. Table for Primitive root for some numbers



ng(n)
21
32
43
52, 3
65
73, 5
92, 5
103, 7
112, 6, 7, 8
132, 6, 7, 11
Subscribe to: Posts (Atom)